数组中的最大数对和

给你一个下标从0开始的整数数组nums。请你从nums中找出和最大的一对数，且这两个数数位上最大的数字相等。
返回最大和，如果不存在满足题意的数字对，返回 -1 。

示例 1：

输入：nums = [51,71,17,24,42] 输出：88 解释： i = 1 和 j = 2 ，nums[i] 和 nums[j]
数位上最大的数字相等，且这一对的总和 71 + 17 = 88 。 i = 3 和 j = 4 ，nums[i] 和 nums[j]
数位上最大的数字相等，且这一对的总和 24 + 42 = 66 。 可以证明不存在其他数对满足数位上最大的数字相等，所以答案是 88 。

示例 2：

输入：nums = [1,2,3,4]
输出：-1
解释：不存在数对满足数位上最大的数字相等。

提示：
2 <= nums.length <= 100
1 <= nums[i] <= 104

思路：
首先根据nums.length可以知道数据范围并不大，因此我们可以直接暴力枚举整数数组nums中的两个数，判断这两个数数位上最大的数字是否相等。维护一个maxx用于存储最大和，若满足条件，即这两个数数位上最大的数字相等，则更新maxx。
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxSum(vector<int>& nums) {
        int maxx=-1;
        for(int i=0;i<nums.size();i++){
            for(int j=i+1;j<nums.size();j++){
                int ma1=0,ma2=0,tmp1=nums[i],tmp2=nums[j];
                while(tmp1){
                    ma1=max(ma1,tmp1%10);
                    tmp1/=10;
                }
                while(tmp2){
                    ma2=max(ma2,tmp2%10);
                    tmp2/=10;
                }
                if(ma1==ma2)maxx=max(maxx,nums[i]+nums[j]);
            }
        }
        return maxx;
    }
};

翻倍以链表形式表示的数字

给你一个 非空 链表的头节点 head ，表示一个不含前导零的非负数整数。
将链表 翻倍 后，返回头节点 head 。
示例 1：
在这里插入图片描述

输入：head = [1,8,9]
输出：[3,7,8]
解释：上图中给出的链表，表示数字 189 。返回的链表表示数字 189 * 2 = 378 。

示例 2：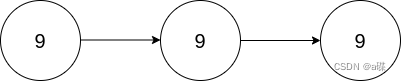
在这里插入图片描述

输入：head = [9,9,9]
输出：[1,9,9,8]
解释：上图中给出的链表，表示数字 999 。返回的链表表示数字 999 * 2 = 1998 。

提示：
链表中节点的数目在范围 $[1, 10^4]$ 内
$0 <= Node.val <= 9$
生成的输入满足：链表表示一个不含前导零的数字，除了数字 0 本身。

思路：
这道题主要考察的是对链表的操作，既然要对链表翻倍，那么我们一定要考虑到进位如何表示，可以先将链表进行翻转，翻转之后对链表的各个数字进行翻倍的操作会变得简单一些。最后再将链表翻转回来即可。
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode *reverse(ListNode *p){
        ListNode *q=NULL;
        while(p){//链表翻转
            ListNode *x=(ListNode*)malloc(sizeof(ListNode));
            x->val=p->val;
            if(q==NULL){
                q=x;
                q->next=NULL;
            }
            else{
                x->next=q;
                q=x;
            }
            p=p->next;
        }
        return q;
    }
    ListNode* doubleIt(ListNode* head) {
        int num=0;
        ListNode *p,*x,*q;
        p=head;
        q=reverse(p);
        ListNode *h=q;
        int pre=0;
        while(q){//将链表进行翻倍
            int k=q->val;
            k*=2;
            q->val=k%10+pre;
            pre=k/10;//加在下一位上
            q=q->next;
        }
        h=reverse(h);
        if(pre){//如果最高位也需要进位
            x=(ListNode*)malloc(sizeof(ListNode));
            x->val=pre;
            x->next=NULL;
            x->next=h;
            h=x;
        }
        return h;
    }
};

限制条件下元素之间的最小绝对差

给你一个下标从 0 开始的整数数组 nums 和一个整数 x 。
请你找到数组中下标距离至少为 x 的两个元素的 差值绝对值 的 最小值 。
换言之，请你找到两个下标 i 和 j ，满足 abs(i - j) >= x 且 abs(nums[i] - nums[j]) 的值最小。
请你返回一个整数，表示下标距离至少为 x 的两个元素之间的差值绝对值的 最小值 。
示例 1：

输入：nums = [4,3,2,4], x = 2
输出：0 解释：我们选择 nums[0] = 4 和 nums[3] = 4 。
它们下标距离满足至少为 2 ，差值绝对值为最小值 0 。 0 是最优解。

示例 2：

输入：nums = [5,3,2,10,15], x = 1
输出：1
解释：我们选择 nums[1] = 3 和 nums[2] = 2 。 它们下标距离满足至少为 1 ，差值绝对值为最小值 1 。 1 是最优解。

示例 3：

输入：nums = [1,2,3,4], x = 3
输出：3
解释：我们选择 nums[0] = 1 和 nums[3] = 4 。它们下标距离满足至少为 3 ，差值绝对值为最小值 3 。 3 是最优解。

提示：
$1 <= nums.length <= 10^5$
$1 <= nums[i] <= 10^9$
$0 <= x < nums.length$

思路：
看到数据范围，知道暴力枚举方法必定会时间超限，看到两个下标，我第一眼想到的就是双指针，滑动窗口的方法。当我们处理第i个数的时候，如果i+x以及之后的数是有序的，那么我们可以通过二分很快计算出最接近与nums[i]的数。
如何维护这个有序的序列呢。数据结构set可以保证集合的有序，使用multiset可以保证序列中存在重复的数字。
所以我们初始化一个multiset，命名ms，一开始将从x位置往后的所有数字都插入ms中。从下标为0的位置i开始逐一枚举，找到和其下标距离大于等于x且与其最相近的一个数，可以使用lower_bound找到第一个大于等于该数的数a。但是与此同时，我们还需要考虑这个数字a的前一个数字(即小于该数的最大的数)，计算这两个数和nums[i]的差值，维护最小值即可。
然后开始移动窗口，往右移动一格，则第i+x的数需要移出，因为距离小于x了。然后还需要将i+1-x位置的数移入，因为该位置距离为x。
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minAbsoluteDifference(vector<int>& nums, int x) {
        if(x==0)return 0;
        multiset<int>ms;//用来维护一个有序的集合
        int n=nums.size();
        for(int i=x;i<n;i++)ms.insert(nums[i]);
        int ans=1e9;
        for(int i=0;i<n;i++){
            auto it=ms.lower_bound(nums[i]);//找到后面的大于等于nums[i]的最小的数字
            if(it!=ms.end())ans=min(ans,*it-nums[i]);
            if(it!=ms.begin())ans=min(ans,nums[i]-*prev(it));//找到该数字的前一个数字
            //移动窗口
            if(i+x<n)ms.erase(ms.find(nums[i+x]));//往后移动，移除
            if(i+1-x>=0)ms.insert(nums[i+1-x]);//这个位置的数也符合要求了
        }
        return ans;
    }
};